VM programmed with TCP packet timing - nvm (rev) from justCTF 2023
This post is a writeup for a challenge I was working on during justCTF 2023. I didn’t solve it during the competition, unfortunately. But I decided to take a look at it afterwards, as it seemed interesting! (and I also needed some rev challenge for a class in the university :D)
Description
Some time ago I hosted a service that allowed me to do calculations on my computer. One day I noticed someone was executing the same code over and over again. After analyzing the network traffic, I noticed that only the initial packets change.
Can you find out what’s going on?
Author: Rivit
| Files: | nvm.zip |
| Solves: | 11 |
| Points: | 355 |
Approach
The handout consists of 3 files:
Dockerfile- copy the binary to aubuntu:22.04container and run itworker- ELF binary, we need to figure out what it does :)trace.pcap- network capture of a communication with the binary?
Opening the pcap in Wireshark we can see one TCP stream with some custom protocol:
Upon connection the server sends RDY, then the client sends the alphabet??? and after that 2 bytes of data at a time that are acknowledged with OK by the server. Decoding the data didn’t result in anything, time to dig into the binary.
Reversing and cheesing attempt
Let’s open the binary in Binary Ninja. It is fully stripped and written in C++ 🥲.
Quickly skimming over the binary we find some interesting strings.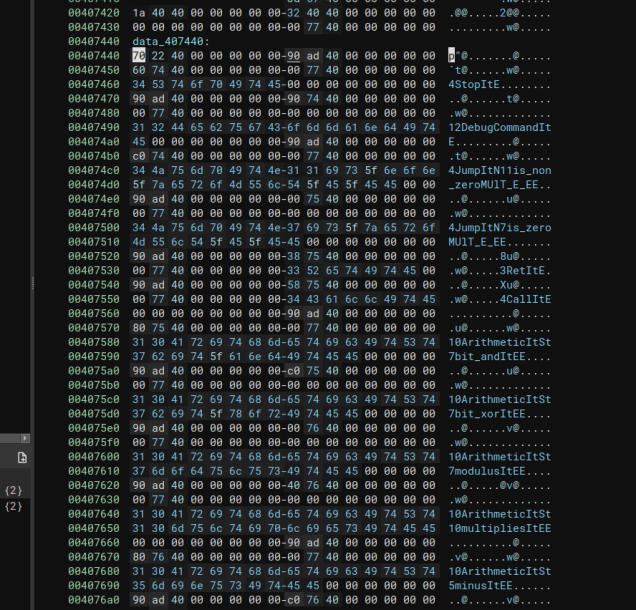
Only at this point have I realized that the name of this challenge refers to a virtual machine that is implemented inside the binary and programmed over TCP. So I thought: “Hmm, might be fastest to just replay the pcap and see what the binary does”. So I quickly implemented a python script to replay the pcap in pwntools. And… the binary didn’t do anything? Huh. That’s super weird. So no other option but to reverse the whole binary I guess. Dynamic analysis can only go so far.
Real reversing
The main function was easy to find. From there we identify the socket setup and then the loop handling the connection. A few functions in, I identified the function reading the bytecode bytes from the connection: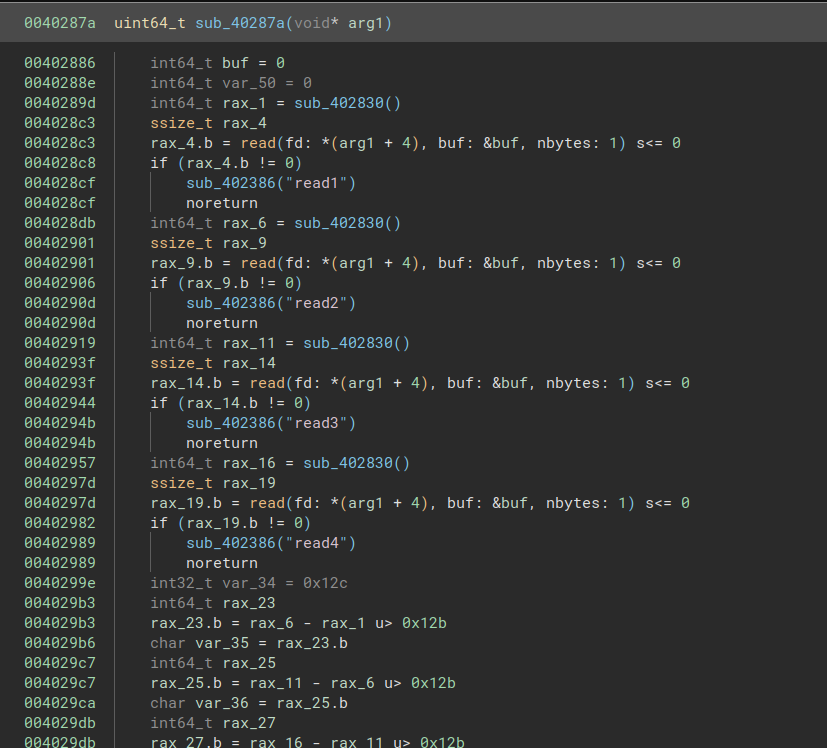
The arg1 is a pointer to the global program object from which the fd is read. We can see that the stream is read one byte at a time - 4 bytes are read in total in the function. But… where do the bytes go?? I was very confused by this. I tried decompiling in IDA and Ghidra, looking into the assembly, just to be sure I’m not missing something. But no. The byte is read into the buf buffer. But buf is not used anywhere.

Well, spoiler alert. The answer lies in the function called in-between the reads. This is a great example of why it is important to rely on more than one tool.
Binary Ninja decompiles the function like this: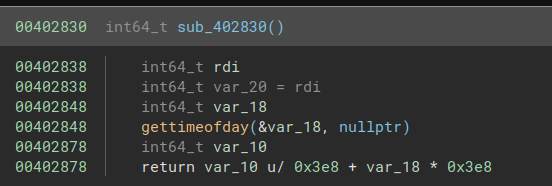
This looks confusing and tbh caused me to ignore this function for a while, thinking it was bullocks. IDA knows what arguments gettimeofday takes and decompiles this like: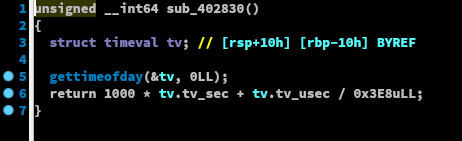
Okay, I see! This returns the current timestamp in milliseconds! The return values are used in the construction of the final (half-)byte (I’m switching to my annotated version of the binary here):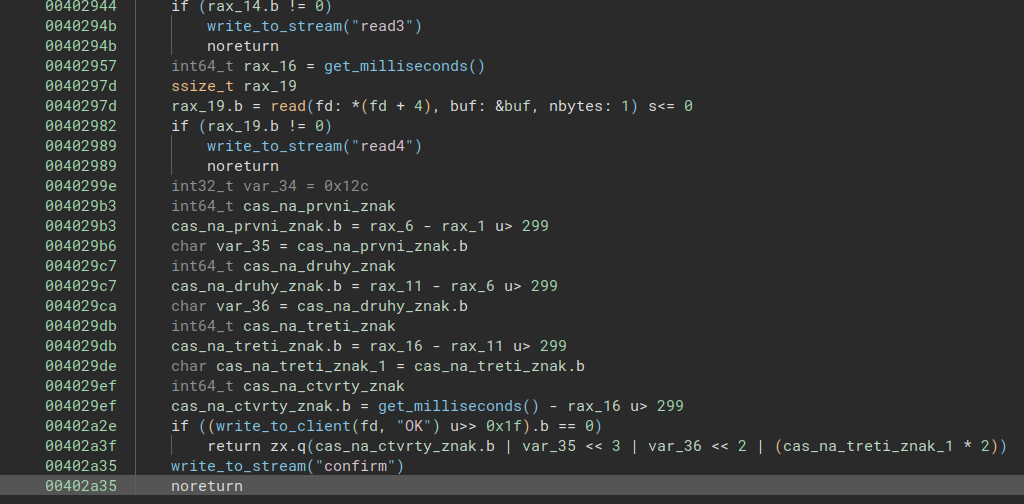
Anything below 299 milliseconds between bytes is considered a 0, anything above a 1. In the pcap, we see that the bytes are sent in individual packets, so that’s why this is possible.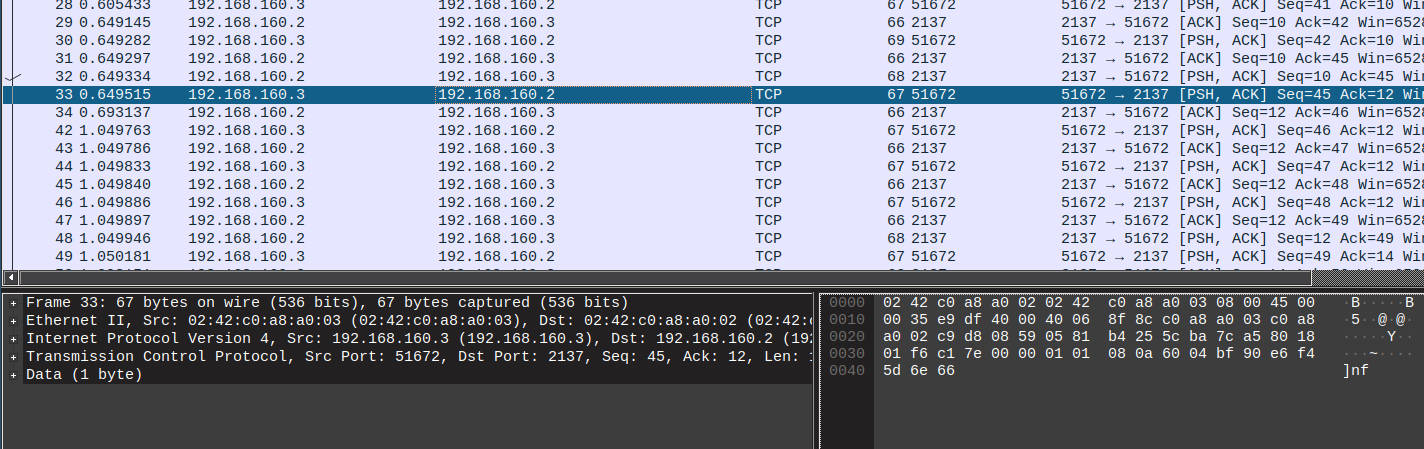
It’s the timing between the packets that matters!
Every byte transmitted is a bit of the program for the VM. After this was clear, I could focus on the actual VM reversing.
The actual VM reversing
I quickly identified the familiar OP code switch statement: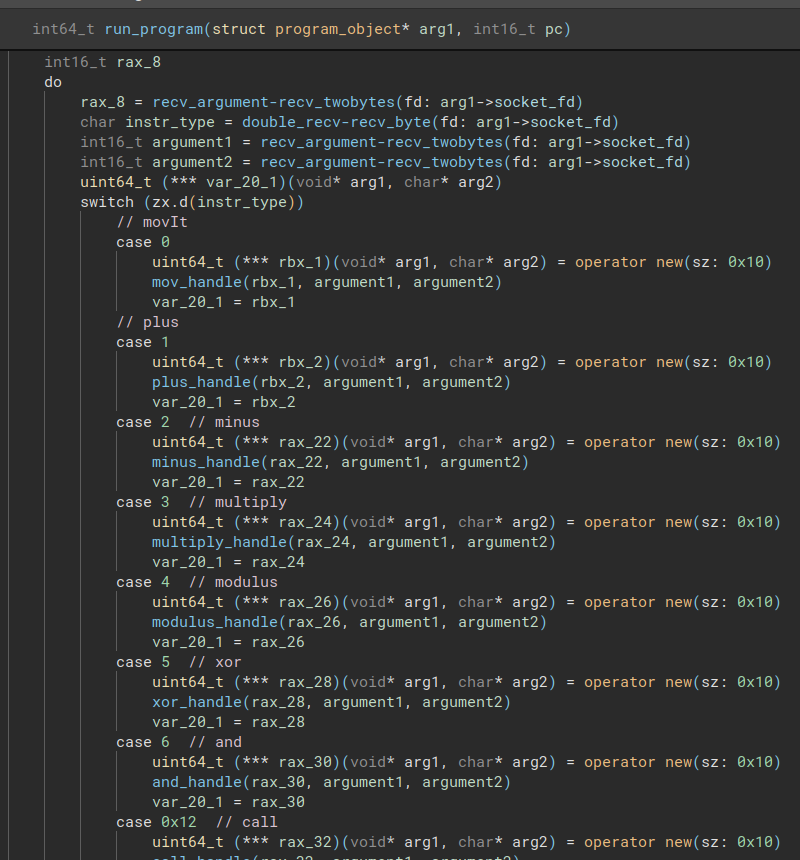
The handlers here are just adding the correct instruction objects to the program on the address received in rax_8. So we need to figure out the corresponding instruction evaluators from pointers in the vtables defined in the .rodata section.
We figure out we are dealing with a 16-bit Harvard architecture machine. What I called the app_object that represents the state of the machine and is passed all over the place has the following structure: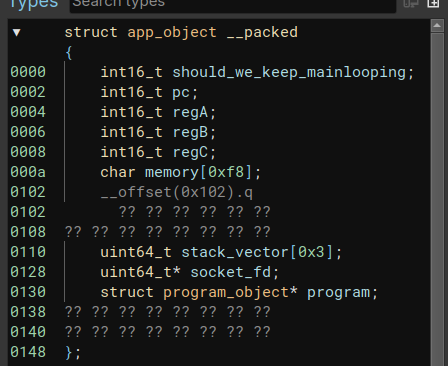
4 registers, some memory, and a stack (used for tracking function calls) - pretty neat. The first 0x20 bytes received (the bytes themself, not timing bits this time - so the alphabet in the pcap) are written to the beginning of the memory. Interesting.
The instruction set is the following:
movaddsubmlpmodxorandcalretjzjnzjdg- debug: dump everythinghlt- stop execution
Almost all arithmetic instructions have different modes of operation. One operating on registers, the other with a register and immediate value, a register and memory etc. These are set by 2 modifier bits in each instruction. They all follow a similar pattern across the instructions. For example the add instruction:
| MB | Operation |
|---|---|
| 0 | regA = regA OP regB |
| 1 | regA = regA OP imm |
| 2 | regA = regA OP mem |
| 3 | mem = mem OP regB |
Note that “memory” in this case means double dereferencing an address stored in a register - the register index is what is stored in the program.
With this knowledge, I’ve first written a script to dump the program ROM from the pcap to a file. And then wrote a disassembler for it. This has given me a nice disassembly of the program: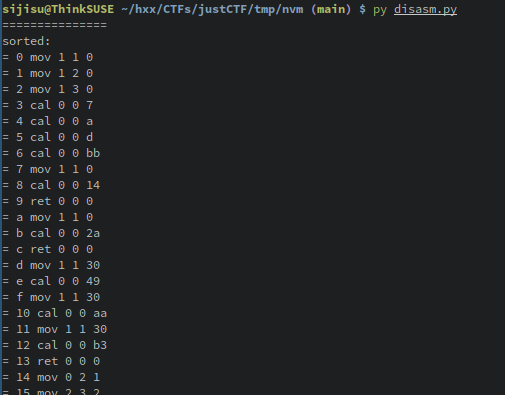
This is as far as I got during the CTF, now fast forward 3 months later…
Finally, the actual reversing
Having the code that the VM is running, now it’s time to dig into what it does.
From the description I strongly suspected that the alphabet - the first bytes received - is the flag and the rest is a flag checker. Looking into the code, it seemed to confirm my suspicion.
As I find it hard to see any patterns in an unfamiliar assembly, I’ve written an emulator for the VM. I also divided the code into “functions”.
With the power of the emulator, we can see first some calculations being performed on the flag and then the result is turned into either a 1 or 0 for each word. A flag checker indeed. We can locate the original flag at address 0x00 and the calculations space for the flag checker at address 0x30.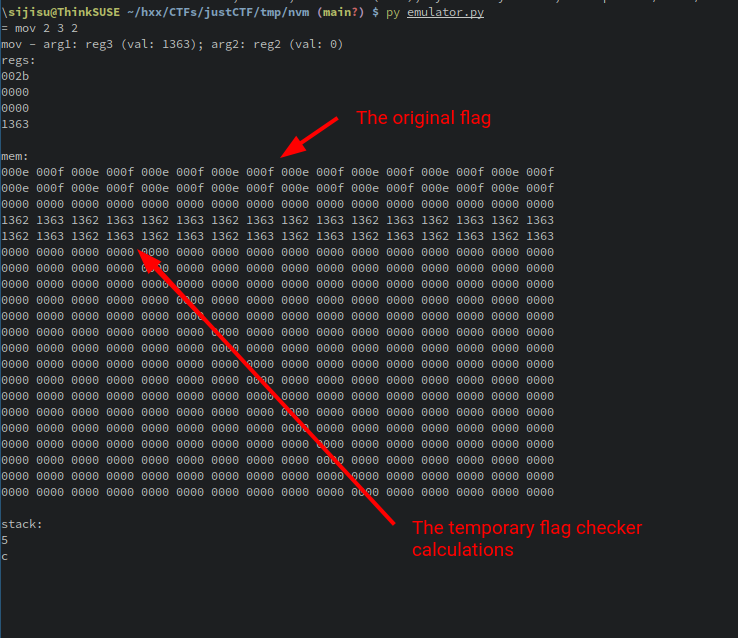
Analysing the program we find the final result checking at address 0x49:
= 49 mov 1 2 c3 // 7
= 4a sub 3 1 2
= 4b add 1 1 1
= 4c mov 1 2 de
= 4d sub 3 1 2
= 4e add 1 1 1
= 4f mov 1 2 2c
...
It compares the hardcoded values to the results of the calculations in memory. So how are those performed? There are two calculation (or should I say obfuscation) functions.
The first is located at 0x14:
= 14 mov 0 2 1 // 2
= 15 mov 2 3 2
= 16 add 1 2 1
= 17 mod 1 2 20
= 18 add 2 3 2
= 19 add 1 2 1
= 1a mod 1 2 20
= 1b add 2 3 2
= 1c add 1 1 30
= 1d add 1 3 1337
= 1e xor 3 1 3
= 1f sub 1 1 30
= 20 add 1 1 1
= 21 mod 1 1 20
= 22 jnz 0 1 14
= 23 ret 0 0 0
This will for ith position compute the following:
tmp[i] = flag[i%0x20]+flag[(i+1)%0x20]+flag[(i+2)%0x20]+0x1337
A simple sum of 3 following flag bytes + a constant.
The second is called afterwards and is located at 0x2a:
= 2a mov 0 2 1 // 4
= 2b mov 2 3 2
= 2c add 1 2 1
= 2d mod 1 2 20
= 2e add 2 3 2
= 2f cal 0 0 39
= 30 mov 1 3 30
= 31 add 0 3 1
= 32 xor 3 3 2
= 33 mov 1 2 ff
= 34 and 3 3 2
= 35 add 1 1 1
= 36 mod 1 1 20
= 37 jnz 0 1 2a
= 38 ret 0 0 0
This one seems more complicated as it at 0x2f calls another function. Let’s see what it calls:
= 39 mov 1 2 7f // 5
= 3a mov 3 2 1
= 3b mov 0 2 3
= 3c sub 1 2 1
= 3d mov 0 1 2
= 3e mlp 1 1 3
= 3f sub 0 1 3
= 40 jz 0 1 46
= 41 add 1 1 1
= 42 jz 0 1 46
= 43 add 1 1 1
= 44 jz 0 1 46
= 45 jnz 0 1 3c
= 46 mov 1 3 7f
= 47 mov 2 1 3
= 48 ret 0 0 0
I stared at this and the emulator for some while, but then it clicked. The three jz after each other and mlp before that did it for me. This function divides by 3. It is kinda odd to have it implemented this way, especially when we have a special mod instruction, but it is exactly what it does.
Knowing this, we can rewrite the second calculation function as:
tmp[i] = (tmp[i] ^ ((flag[i%0x20]+flag[(i+1)%0x20])/3))&0xff
We hopefully have all that we need to recover the flag now.
Z3 solver
We know the target values, and we know the formula for how they were calculated from the flag. All there’s left to figure out is what input does produce such target values. If we have enough information about the input, we will recover it and thus get the flag!
SAT solvers and specifically the Z3 solver are made exactly for tasks like this. We prepare the targets extracted from the disassembly. Prepare an array of 32 16-bit BitVectors. Specify the relationships between them. Other than the formula above, we also know that the flag will be one byte per character only and that the first letter should be j (justCTF{...} is the flag format) - this will limit the number of solutions to only the correct one.
| |
After a bit of fiddling with the constrains, we got it!
Flag: justCTF{1t_1s_c4ll3d_4_n000b_vm}
I’ve published all scripts and the Binary Ninja project on my GitLab.
Published on
